Non-Maximum Suppression for Gaussian Pulse Detection

This example demonstrates the use of the NonMaximumSuppression class to detect Gaussian pulses in a one-dimensional signal. It generates a synthetic dataset of Gaussian pulses, applies the non-maximum suppression algorithm, and plots the results.

from DeepPeak.algorithms import NonMaximumSuppression
from DeepPeak.algorithms import ClosedFormSolver
from DeepPeak.signals import SignalDatasetGenerator
from DeepPeak import kernel

NUM_PEAKS = 4
SEQUENCE_LENGTH = 400
NSAMPLES = 4
gaussian_width = 0.03

kernel = kernel.Lorentzian(
    amplitude=(50, 100),  # Amplitude range
    position=(0.1, 0.9),  # Peak position range
    width=gaussian_width,  # Width range
)

generator = SignalDatasetGenerator(n_samples=NSAMPLES, sequence_length=SEQUENCE_LENGTH)

dataset = generator.generate(
    kernel=kernel,
    n_peaks=NUM_PEAKS,
    noise_std=0.3,  # Add some noise
    categorical_peak_count=False,
)

dataset.plot()

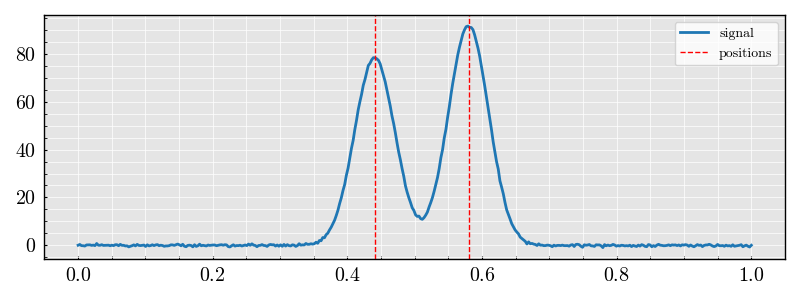
<Figure size 800x900 with 3 Axes>

Configure and run the detector

peak_locator = NonMaximumSuppression(
    gaussian_sigma=0.003,
    threshold="auto",
    maximum_number_of_pulses=NUM_PEAKS,
    kernel_truncation_radius_in_sigmas=3,
)

batched_peak_detector = peak_locator.run_batch(time_samples=dataset.x_values, signal=dataset.signals)

batched_peak_detector.plot()

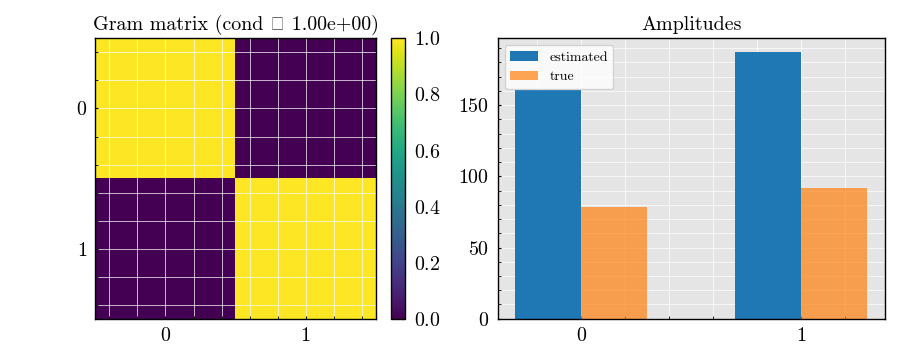
<Figure size 650x1120 with 4 Axes>

Solve for amplitudes

solver = ClosedFormSolver(sigma=dataset.widths.mean().squeeze())

result = solver.run_batch(centers=batched_peak_detector.peak_times, center_samples=batched_peak_detector.peak_amplitude_raw)

result.compare_plot(true_amplitudes=dataset.amplitudes)

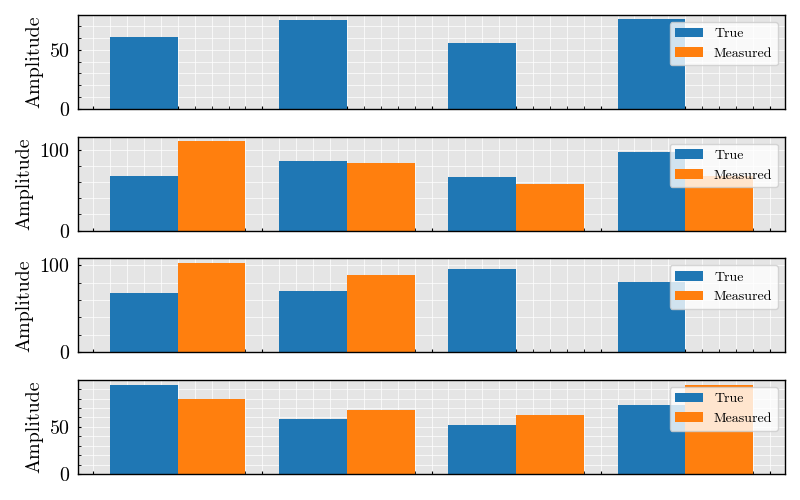
<Figure size 800x500 with 4 Axes>