Gradient of array

In this example, we calculate the gradient of a 2D array using finite difference methods. We will explore different orders of derivatives and visualize their effects on the input array.

Importing required packages

Here we import the necessary libraries for numerical computations, rendering, and finite difference operations.

import numpy as np
from PyFinitDiff.finite_difference_2D import get_array_derivative, Boundaries
import matplotlib.pyplot as plt
from PyFinitDiff import BoundaryValue

Creating the input mesh

We define a 2D Gaussian mesh using two 1D exponential arrays.

idx = np.linspace(-5, 5, 100)
x_array = np.exp(-idx**2)
y_array = np.exp(-idx**2)

y_array, x_array = np.meshgrid(x_array, y_array)

mesh = x_array * y_array

Setting boundary conditions

Define boundary conditions for the gradient calculation. Here, we use ‘none’ for all boundaries.

boundaries = Boundaries(top=BoundaryValue.NONE, bottom=BoundaryValue.NONE, left=BoundaryValue.NONE, right=BoundaryValue.NONE)

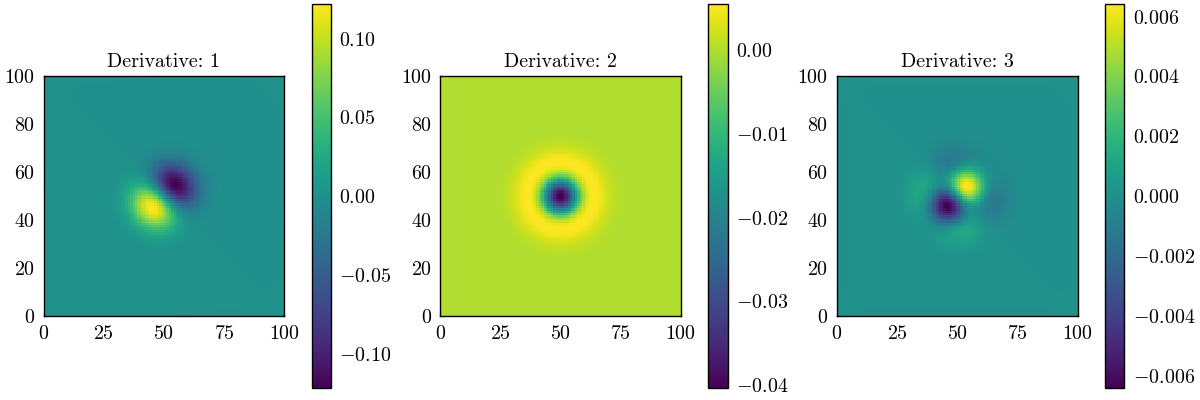
Visualizing the gradient for different derivatives

We compute the gradient for first, second, and third derivatives and visualize them.

figure, axes = plt.subplots(1, 3, figsize=(12, 4), constrained_layout=True)
axes = axes.flatten()

for ax, derivative in zip(axes, [1, 2, 3]):
    gradient = get_array_derivative(
        array=mesh,
        accuracy=6,
        derivative=derivative,
        x_derivative=True,
        y_derivative=True,
        boundaries=boundaries
    )

    image = ax.pcolormesh(gradient.real, shading='auto', cmap='viridis')
    ax.set_title(f'Derivative: {derivative}')
    ax.set_aspect('equal')
    plt.colorbar(image, ax=ax)

plt.show()