Particle Distribution

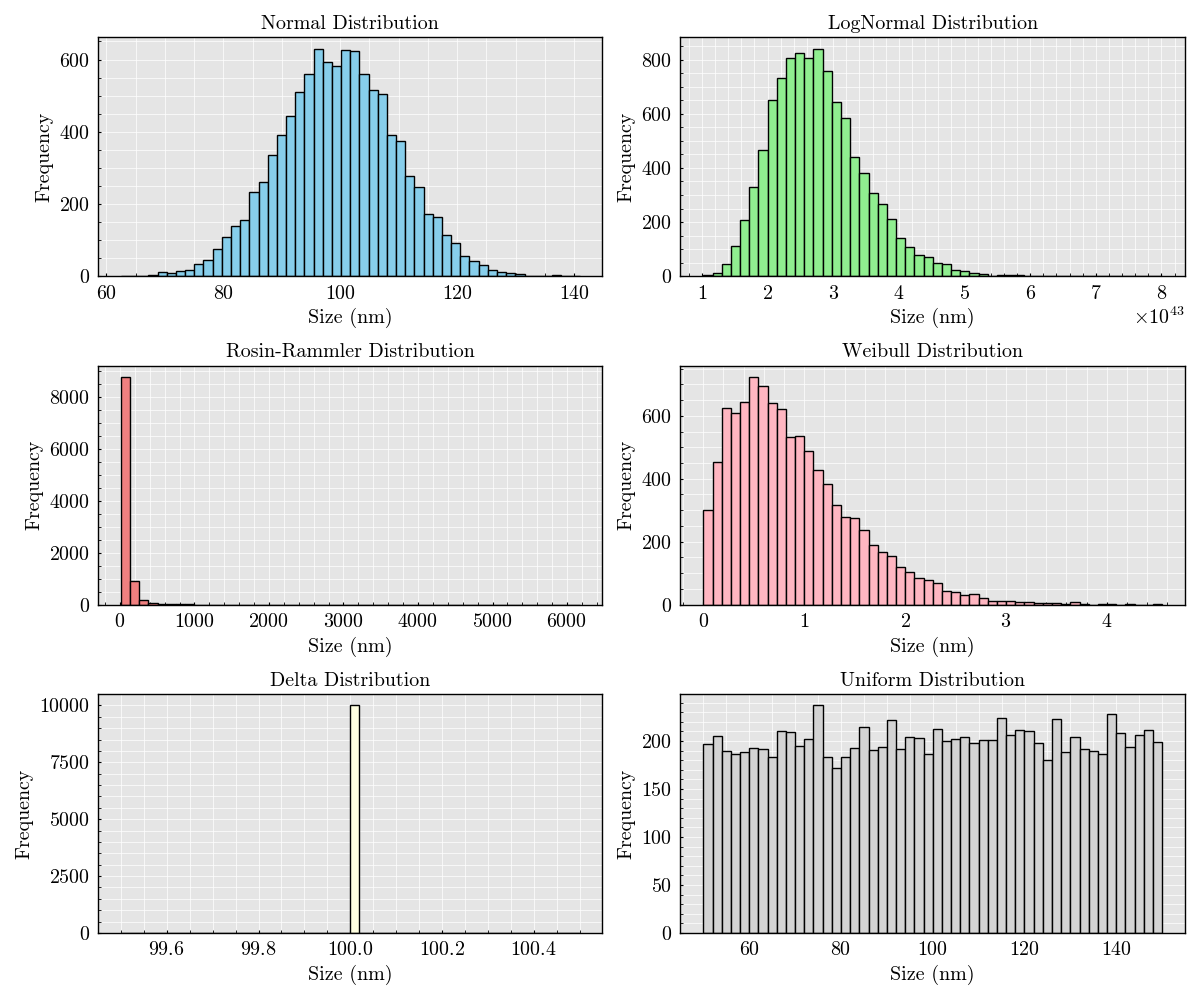
This script demonstrates how to visualize various particle diameter distributions from the FlowCyPy library. It generates and plots particle diameters based on different statistical distributions, such as Normal, LogNormal, Weibull, and more.

Workflow Summary: 1. Initialize particle diameter distributions (Normal, LogNormal, Rosin-Rammler, Weibull, Delta, Uniform). 2. Generate random particle diameters for each distribution. 3. Plot the histograms of each distribution to visualize the spread of particle diameters.

Distributions Covered: - Normal Distribution: Sizes follow a normal (Gaussian) distribution. - LogNormal Distribution: Sizes follow a log-normal distribution. - Rosin-Rammler Distribution: Skewed distribution commonly used for particle diameter modeling. - Weibull Distribution: Flexible distribution used in particle modeling. - Delta Distribution: All particles are of a fixed diameter. - Uniform Distribution: Sizes are uniformly distributed between a minimum and maximum value.

Import necessary libraries

import numpy as np
import matplotlib.pyplot as plt
from FlowCyPy import distribution
from FlowCyPy.units import nanometer

# Set random seed for reproducibility
np.random.seed(3)

# Define the number of particles to generate
n_particles = 10000

# Initialize subplots for the distribution plots
fig, axes = plt.subplots(3, 2, figsize=(12, 10))
axes = axes.ravel()

# 1. Normal Distribution
normal_dist = distribution.Normal(mean=100 * nanometer, std_dev=10 * nanometer)
normal_diameters = normal_dist.generate(n_particles)
axes[0].hist(normal_diameters, bins=50, color='skyblue', edgecolor='black')
axes[0].set_title('Normal Distribution')
axes[0].set_xlabel('Size (nm)')
axes[0].set_ylabel('Frequency')

# 2. LogNormal Distribution
lognormal_dist = distribution.LogNormal(mean=100 * nanometer, std_dev=0.25 * nanometer)
lognormal_sizes = lognormal_dist.generate(n_particles)
axes[1].hist(lognormal_sizes, bins=50, color='lightgreen', edgecolor='black')
axes[1].set_title('LogNormal Distribution')
axes[1].set_xlabel('Size (nm)')
axes[1].set_ylabel('Frequency')

# 3. Rosin-Rammler Distribution
rosinrammler_dist = distribution.RosinRammler(characteristic_property=50 * nanometer, spread=2.0)
rosinrammler_sizes = rosinrammler_dist.generate(n_particles)
axes[2].hist(rosinrammler_sizes, bins=50, color='lightcoral', edgecolor='black')
axes[2].set_title('Rosin-Rammler Distribution')
axes[2].set_xlabel('Size (nm)')
axes[2].set_ylabel('Frequency')

# 4. Weibull Distribution
weibull_dist = distribution.Weibull(scale=50 * nanometer, shape=1.5 * nanometer)
weibull_sizes = weibull_dist.generate(n_particles)
axes[3].hist(weibull_sizes, bins=50, color='lightpink', edgecolor='black')
axes[3].set_title('Weibull Distribution')
axes[3].set_xlabel('Size (nm)')
axes[3].set_ylabel('Frequency')

# 5. Delta Distribution
delta_dist = distribution.Delta(position=100 * nanometer)
delta_sizes = delta_dist.generate(n_particles)
axes[4].hist(delta_sizes, bins=50, color='lightyellow', edgecolor='black')
axes[4].set_title('Delta Distribution')
axes[4].set_xlabel('Size (nm)')
axes[4].set_ylabel('Frequency')

# 6. Uniform Distribution
uniform_dist = distribution.Uniform(lower_bound=50 * nanometer, upper_bound=150 * nanometer)
uniform_sizes = uniform_dist.generate(n_particles)
axes[5].hist(uniform_sizes, bins=50, color='lightgray', edgecolor='black')
axes[5].set_title('Uniform Distribution')
axes[5].set_xlabel('Size (nm)')
axes[5].set_ylabel('Frequency')

# Adjust layout
plt.tight_layout()
plt.show()